Aspect Ratio Calculator

Aspect Ratio Calculator

Every frame, digital video, screen, responsive design and image often has a rectangular shape that is exceptionally accurate in proportion (or ratio). Adjusting proportions across different media is often a challenge for designers, especially if they have to crop and transform content. We made a quick and easy aspect ratio calculator for you to throw in your image dimensions and get the aspect ratio calculator data to help you resize images better in Photoshop or whatever tool you are using. It works great for both photos and videos. If you are working with digital video, you must first compress the digital video files to get the exact dimensions (or aspect ratios) of the video.

Understanding photo and image dimensions requires a bit of calculation. And that’s where an aspect ratio calculator comes in to help make these calculations accurate. To get accurate video aspect ratios, simply input one dimension and the calculator will calculate the other.

What is aspect ratio?

Aspect ratio is an attribute of image projection that describes the proportional relationship between the width and height of the image. Essentially, it describes the shape of the image. Aspect ratios are written as a formula of width to height: 3:2.

For example, movies, which are usually shot with a wide angle lens, have an aspect ratio that is typically 16:9, which means that the width of the image area is almost twice as wide as its height. The traditional television and computer screen, on the other hand, are designed for an aspect ratio of 1.33:1, which means that the width of the viewing area is only 1.33 times its almost square height. A mismatch between the aspect ratio of a movie and television usually means a compromise in the size or fullness of the picture when watching a movie on a regular television. Many newer television screens, such as those using HDTV technology, are widescreen with a 16:9 aspect ratio.

Aspect ratios are written as a formula of width to height: 3:2. For example, a square image has an aspect ratio of 1:1 because the height and width are the same. The image could be 500px × 500px, or 1500px × 1500px, and the aspect ratio would still be 1:1.

As another example, a portrait-style image might have an aspect ratio of 2:3. With this aspect ratio, the height is 1.5 times the width. Thus, the image could be 500px × 750px, 1500px × 2250px, etc.

How to calculate aspect ratio

To calculate aspect ratio of an image, you divide the height by the width. The formula is Height * Width / Height. We use the below code to calculate aspect ratio in our tool. It’s basically saying when we ask for the GCD of (x,y), return us the ratio(width,height). In this instance, x = width and y = height of our image or device.

{
     function ratio(x,y) {c=gcd(x,y); return ""+(x/c)+":"+(y/c)};
     return ratio(width,height);
}

How to calculate aspect ratio in Excel

Microsoft Excel is a great tool for working with numbers and mathematical formulas. Using the formula below we can quickly batch calculate our aspect ratios for given sets of images. This is actually how we calculated all the aspect ratios on our mobile devices table.

Excel uses a function called the GCD. The greatest common divisor of two or more numbers. The GCD is the largest possible number that can go in to your image dimension without a remainder (or fraction). For example, =GCD(60,36) = 12. GCD is calculated automatically in Excel when you use the GCD function in a cell. In longform, it is working out the prime factorisations of the two numbers and comparing the lowest possible results.

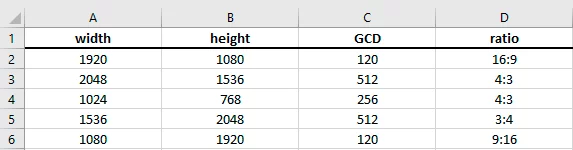
To test out GCD in Excel, use the below function, which gives us the result of 120 (shown in C2 in the above image):

=GCD(A2,B2)

Now, to calculate the aspect ratio in Excel, use the below function which returns a results of 16:9 in D2.

=A2/GCD(A2,B2)&":"&B2/GCD(A2,B2)

There’s some more interesting discussions on calculating aspect ratios using code here and here.